An R Package for Social Roulette
Abstract:
We introduce the R package socialroulette, which is a lightweight package for handling the recurrent problem of assigning individuals into groups of a fixed size. In order to minimize reunions, we provide an algorithm to solve the task as an instance of the maximally diverse grouping problem.

 This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The R-markdown
source code of this blog is available under a GNU General Public
License (GPL v3) license from GitHub.
This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The R-markdown
source code of this blog is available under a GNU General Public
License (GPL v3) license from GitHub.
Introduction
Groupings are relevant when breakout rooms, mystery lunch partitions or student peer review groups are made. My last blog post Long time, no see: Virtual Lunch Roulette considered the probability of being assigned into the same group as someone, you already were in the same group with the last time (aka. a re-union) when using simple random sampling to assign the groups. This probability proved to be surprisingly high.
In this post we develop the subject further by introducing the R
package socialroulette,
which aims at being helpful in making better group assignments based on
solutions of the maximally
diverse grouping problem (MDGP) known from operations
research.
The Problem
The aim is to partition \(n\) participants into groups of size at least \(m\). We shall denote the resulting groupings a partition of the set of \(n\) participants. If \(m\) is not a divisor of \(n\) then some of the groups have to contain more than \(m\) participants. As an example consider the case that 5 individuals are to be divided into groups of size at least 2. We shall adopt the convention, that group size shall be as close to \(m\) as possible and the group sizes should be as equal as possible. In the specific toy example this means that we will need 2 groups, one with 3 participants and one with 2 participants.
When assigning such groups repeatedly, e.g. one a weekly basis, an additional criterion can be to form the groups, such that as few participants as possible are assigned into groups with individuals they were already in the same group with previously. This can, e.g., be done by rejection sampling. However, as situations can occur where such re-unions are unavoidable, it can instead be natural to formulate a metric to maximize, which quantifies penalities due to such re-unions. As an example: If one has to decide between assigning two individuals to the same group who met 7 days or 14 days ago, it might be preferable to choose the pair which met 14 days ago. Such optimization is known as solving the maximally diverse grouping problem (see appendix).
The R package socialroulette
We illustrate the package by considering a use-case, where a class of
students repeatably for every lecture have be assigned into breakout
rooms. First, we install and load the socialroulette
package available from GitHub.
# Install package
devtools::install_github("hoehleatsu/socialroulette")
library(socialroulette)Note: A binary package version is available from my r-universe, which is a pipeline automatically compiling the package through GitHub actions.
Say the class consists of 100 students, which for a weekly virtual lab exercise class need to be divided into groups of at least 4. Since for various reasons not all students show up for each class, the sampling frame of individuals to be partitioned each week changes accordingly. Still, we would like to make the partitioning of the current week s.t. students get as many new acquaintances as possible.
We first create a history of the previous 4 weeks’ groupings as well as the frame of participants for the current lecture.
# Class of 100 students with 4 previous lectures
students <- tibble::tibble(id=sprintf("id%.3d@student.su.se", 1:100))
partition_dates <- seq(as.Date("2021-03-31"), length.out=4, by="1 week")
# Simulate changing participation each week for the last 4 weeks (70% attendance)
frames <- map_df( partition_dates, ~
students %>% slice_sample(n = rbinom(1,nrow(.), prob=0.7)) %>%
mutate(date=.x))
# Generate some past partitions using simple random sampling
past_partitions <- frames %>%
group_split(date) %>%
map(~rsocialroulette(current_frame=.x, m=4, algorithm="srs")) %>%
setNames(partition_dates)## Partitioning 72 individuals into groups of at least 4 (no past partitions).
## Created 18 groups of sizes 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4.
## Partitioning 74 individuals into groups of at least 4 (no past partitions).
## Created 18 groups of sizes 5 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4.
## Partitioning 71 individuals into groups of at least 4 (no past partitions).
## Created 17 groups of sizes 5 5 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4.
## Partitioning 69 individuals into groups of at least 4 (no past partitions).
## Created 17 groups of sizes 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4.We pretend that each of the above previous partitions has been saved as a .csv file. For example like:
# Simulate the storage of each partition as a .csv file to disk
# with 3 columns: date, id1 and id2, i.e. all pairs
temp_dir <- tempdir() #adjust path to your setting if needed
socialroulette::partitions_to_pairs( past_partitions ) %>%
group_split(date) %>%
walk(~ write_csv(x=.x, file=file.path(temp_dir, stringr::str_c("socialroulette-", .$date[1], ".csv"))))We thus read the partitions from disk and convert from the stored
pair-format (i.e. a data.frame listing each pair being in
the same group as id1, id2 together with the
corresponding date of the partition) back to the
list-format (i.e. a list of character vectors, where each vector denotes
a group and the vector contains the ids of all members of that group).
This can be done as follows:
# Read again from file
pairs <- map_df(list.files(path=temp_dir, pattern="socialroulette.*", full.names=TRUE), ~read_csv(file=.x))As a next step we sample the students who are in the next class to group.
current_frame <- students %>%
slice_sample(n = rbinom(1,nrow(.), prob=0.7)) %>%
mutate(date=max(partition_dates) + diff(partition_dates) %>% mean())Our goal is now to partition the 71 students in
current_frame. For each of the \({71 \choose 2 }= 2485\) possible pairs of
students in that class, we determine how long ago it has been, since
they were in the same group the last time. This can be done using the
internal package function partitions_to_distance:
dist <- socialroulette::partitions_to_distance(current_frame, past_partitions)
dist %>% head()## # A tibble: 6 x 4
## id1 id2 date dist
## <chr> <chr> <date> <dbl>
## 1 id078@student.su.se id100@student.su.se 2021-04-28 35
## 2 id078@student.su.se id092@student.su.se 2021-04-28 35
## 3 id078@student.su.se id098@student.su.se 2021-04-28 35
## 4 id078@student.su.se id093@student.su.se 2021-04-28 35
## 5 id078@student.su.se id083@student.su.se 2021-04-28 35
## 6 id078@student.su.se id095@student.su.se 2021-04-28 35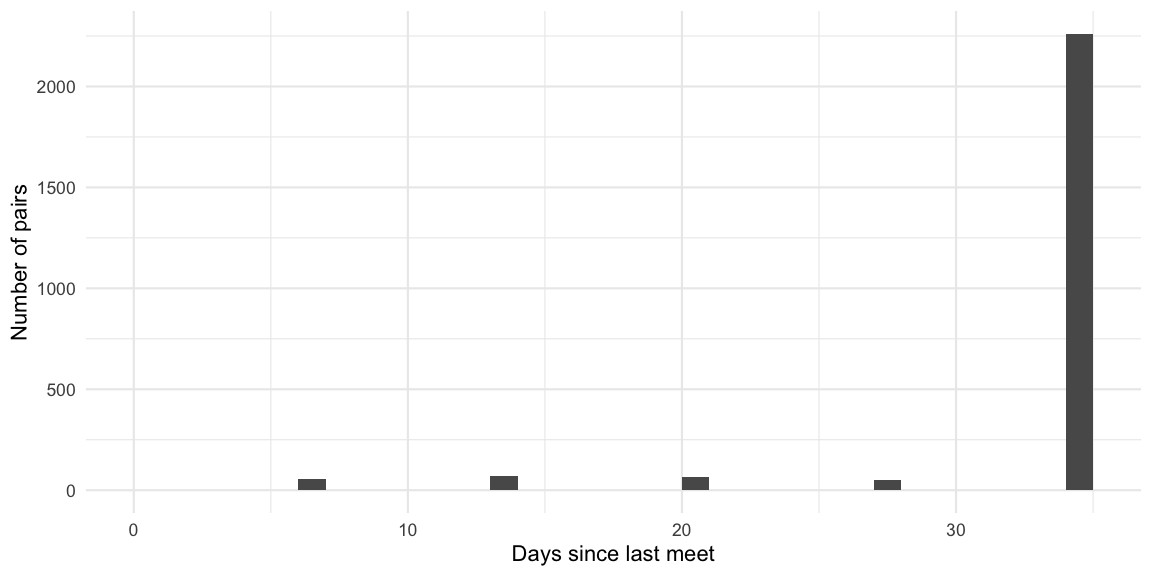
Since the past partitions contain the last 4 weeks, students who have not been in a group so far are assigned a value of one time difference more than the last possible meeting opportunity. In the specific example this corresponds to \(7\cdot (4 + 1) = 35\) days. It thus seems natural to choose the groups, s.t. they do not contain pairs, which have already met in the past. However, for given size of the population, group sizes and meeting histories, this might not be possible to achieve altogether, so a more flexible criterion is to maximize the sum of distance since the last meet over all pairs in the same group.
# Make the partition using a mdgp solver
partition <- rsocialroulette(current_frame, past_partitions, m=4, algorithm="mdgp")The partition can be visualized using the igraph
package:
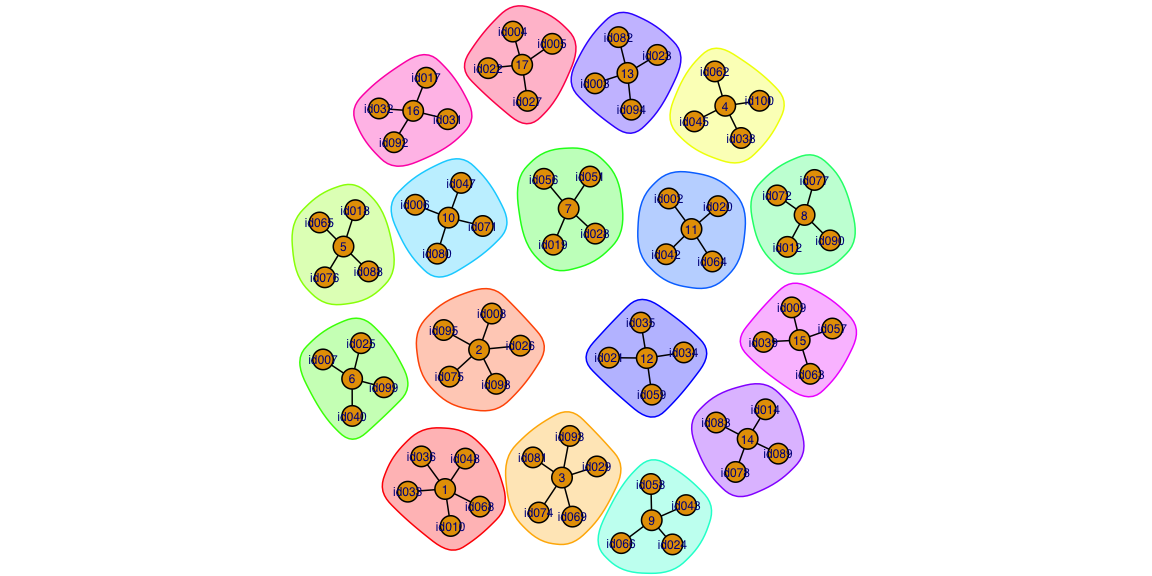
Of course the partition can also be stored to file as before, in order to include it in the set of past partitions when doing the partitioning next week:
list(partition) %>%
setNames(current_frame %>% slice(1) %>% pull(date)) %>%
socialroulette::partitions_to_pairs() %>%
write_csv(file=file.path(temp_dir, stringr::str_c("socialroulette-", .$date[1],".csv")))or can be stored in a Zoom compatible breakout room specification format:
partition %>%
socialroulette::partition_to_frame() %>%
rename(email=id) %>%
mutate(room = sprintf("room%.03d",group)) %>%
select(room, email) %>%
write_csv(file=file.path(temp_dir, stringr::str_c("zoom-breakoutrooms.csv")))Discussion
We provide functionality to create better groupings than obtained by simple random sampling. However, as mathematically convincing the MDGP solution might be, reunions can have their charm.
Acknowledgements
We thank Xiangjing Lai and Jin-Kao Hao for
contributing their C++ source code of the MDGP solver in Lai and Hao (2016)
under a GPL-3 license for the socialroulette
package.
Appendix: Maximally diverse grouping problem
In this appendix we provide a few more mathematically details about the maximally diverse grouping problem, which is about partitioning \(n\) individuals into groups of size at least \(m\) while maximizing a sum of utility values computed by summing the utility \(u(i,j)\) over all individuals \(i\), \(j\) partitioned into the same group.
More formally, let \(d_{ij}\) denote the number of time units (typically days) ago, that individual \(i\) and \(j\) were in the same group. Note: This distance is derived by looking at the previous partitions. It is a matter of definition what this value should be, if \(i\) and \(j\) have not previously been in the same group. Let \(G=n\> \text{div}\> m\) denote the resulting number of groups where \(\text{div}\) denotes integer division. For a given partition let \(x_{ig}\) be an indicator variable, which is 1, if \(i\) is assigned into group \(g\) and zero otherwise.
A solver of the maximally diverse grouping problem now tries to maximize \[ \sum_{g=1}^G \sum_{i=1}^n \sum_{j=i+1}^n d_{ij} x_{ig} x_{jg}, \] subject to the conditions \[ \begin{align*} &\sum_{g=1}^{G} x_{ig} = 1,&& i=1,\ldots,n, \\ &\sum_{i=1}^n x_{ig} = n_g,&& g=1,\ldots,G, \\ &x_{ig} \in \{0,1\}, && i=1,\ldots,n;\quad g=1,\ldots,G, \\ \end{align*} \] where \(n_g\) is the size of group \(g\), i.e. \(\sum_{g=1}^G n_g = n\). We shall adopt the convention that group sizes are determined by assigning the labels \(1,\ldots,G\) to the participants by starting from the first to the last, e.g., as \(((\text{index} - 1) \> \text{mod}\> m) + 1\) and then count how often each label occurs. This means, e.g., that for \(n=7\) and \(m=4\) we get \(n_g=7\> \text{div}\> 4=1\) group with 7 members.
The socialroulette package uses as backend a C++
implementation of MDGP solver of Lai and Hao (2016).