Purr yourself into a math genius
Abstract:
We use the purrr package to solve a popular math puzzle via a combinatorial functional programming approach. A small shiny app is provided to allow the user to solve their own variations of the puzzle.
 This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
Introduction
No. 4 of the Top 5 hard math puzzles at briddles.com goes like this:
Note: a solution has to use each of the specified 4 numbers exactly ONCE, but they can be used in any order. In other words the standard scheme is to solve expressions of the kind:
a op1 b op2 c op3 d
where a, b, c and
d denote a permutation of the numbers 8, 8, 3, 3 and each
of op1, op2 and op3 denotes the
use of one binary operator selected from +, -, * or /. An example is the
expression 8 + 3 + 8 * 3. Parentheses are used to control
the order in which the operators are applied, i.e.
(8 + 3 + 8) * 3 yields a different result than
8 + 3 + (8 * 3).
After a few unsuccessful attempts to solve the above puzzle with pen and paper it felt more efficient and computationally challenging to solve this puzzle via a combinatorial approach: Simply try out all permutations of the 4 numbers, the 4 binary operators and all possible sets of parentheses to combine the operators. One can show that there are at most
\[ \begin{align*} && \text{# permutations of the $k=4$ base numbers} \\ \times && \text{# ways to select with replacement $(k-1)$ binary operators from the set $\{+,-,*,/\}$ }\\ \times && \text{# ways to parenthesize the $(k-1)$ binary operators} \\ &=&k! \times 4^{(k-1)} \times \frac{1}{k} \binom{2k-2}p{k-1} \end{align*} \]
different combinations to choose from 1. As an example: for \(k=4\) the maximal number of unique combinations is 21504.
Strategy
We will use a functional approach to solve the above combinatorial problem. Why?
- because it seems like a good use-case for functional programming,
- because it is important to extend your programming horizon every once in a while, and
- because the
purrrfunctional programming toolkit for R allows you to experiment with this without having to leave the R universe 2.
For those not familar with purrr can find a wonderful
didactic introduction in the useR! 2017
tutorial by Charlotte
Wickham. Furthermore, learning purrr was the 7th most
frequent mentioned package in the #rstats users’ 2019 R
goals. In other words: Attention #rstats new years resolution
makers: reading this post is as obligatory as going to
the gym on 01 Jan!
Solving the Math Puzzle
We will divide-and-conquer the solution along the lines of the number
of combinations formula: Firstly, we will store all permutations of the
\((k-1)\) base numbers in a list
perm. Secondly, we will store all possible combinations of
the \((k-1)\) operators in a list
operators and, thirdly, we generate all possible ways of
putting parentheses around the operators into a list
brackets. Subsequently, we form the Cartesian product of
these three lists and build the corresponding expression for each triple
of permutation, operators and parentheses. Finally, each generated
expression is evaluated. The entire result is a data frame containing
all possible expressions and their associated value obtained when
evaluating the expression.
Permutations of the base numbers
We let the variable base_numbers contain the
specification of the numbers to permute for the expression. The code
should be written general enough so it is possible to use a different
base, e.g., \(k=3\) or \(k=5\).
base_numbers <- c(8,8,3,3)
k <- length(base_numbers)
number_perm <- combinat::permn(base_numbers) %>%
map(setNames, nm=letters[seq_len(k)])
##Slim in case permutations of the base numbers contain duplicates.
perm <- number_perm[!duplicated(map(number_perm, paste0, collapse=""))]For \(k=4\) the first step yields a total 21504 combinations. However, since the numbers 8 and 3 both appear more than once in the base numbers, we can slim the number of permutations from 24 to 6. Hence, there are altogether only 5376 combinations to investigate.
Combinations of the operators
The next step is to make all combinations of the \(k-1\) binary operators needed to combine the \(k\) numbers. We use the string format to represent the operators 3 and thus just need the \(k-1\)’th Cartesian product of the set \(\{+, -, *, /\}\) represented as strings.
opList <- list("+", "-", "*", "/")
##Repeat the opList k-1 times
opsList <- map( seq_len(k-1), ~ opList)
##Form the Cartesian product
operators <- cross(opsList) %>%
map( setNames, nm=paste0("op",seq_len(k-1)))Arrangements of the parentheses
As all the involved operators are binary it becomes clear that finding all possible ways to parenthesize the expression corresponds to finding all binary trees with \(k-1\) leaves. Beautiful recursive code inspiration for how to solve this can be found on leetcode.com. Some adaptation to R and our problem at hand was necessary - the idea is to use recursion in \(k\) and use a hash-map to cache results of previous computations.
##Initialize hashmap to save the results of all binary trees up to n=1 leaves
trees <- list()
trees[["0"]] <- NULL
trees[["1"]] <- list(list(val="node", left=NULL, right=NULL))The rather elegant recursive solution for generating all binary trees with \(n\) leaves works by combining all possible ways to generate subbranches containing \(x\) and \(n-x\) leaves, respectively:
allBinTrees <- function(n) {
##Character version of n, which is used as hash key
n_char <- as.character(n)
##Only compute something if n is not already in the hashlist.
if (is.null(pluck(trees, n_char))) {
trees[[n_char]] <<- list()
##Combine all possible ways to generate bintrees with $i$ and $n-i$ leaves
for (i in 1:(n-1)) {
j = n - i
for (left_tree in allBinTrees(i)) {
for (right_tree in allBinTrees(j)) {
trees[[n_char]][[length(trees[[n_char]]) + 1]] <<- list(val=NULL, left=left_tree, right=right_tree)
}
}
}
} #end if not already in tree list
##Return result from our hashmap
return(pluck(trees, n_char))
}We can test the function for \(n=2\), which yields exactly one tree:
##Manual construction
trees2 <- list(list(val=NULL, left=trees[["1"]][[1]], right=trees[["1"]][[1]]))
all.equal(allBinTrees(n=2), trees2)## [1] TRUEThe result is:
tree2String(allBinTrees(n=2)[[1]]) %>% replaceNodes() %>% addOpNumbers## [1] "(a op1 b)"In the above code segments the function tree2String is a
small helper function to convert the nested list structure to a string -
in this case: (node op node). Furthermore, the function
replaceNodes renames the terms node into the
variables (a op b). The op-strings are
converted into numbered op-strings using
addOpNumbers, i.e. the result becomes
(a op1 b). Details about the helper functions can be found
in the code
on github.
With all preparations in place we can now generate all 5 possible ways to parenthesize the 3 binary operations using the following code:
##Make all possible brackets
bracketing <- map_chr( allBinTrees(n=k),
~ tree2String(.x) %>% addOpNumbers %>% replaceNodes)## [1] "(a op1 (b op2 (c op3 d)))" "(a op1 ((b op2 c) op3 d))" "((a op1 b) op2 (c op3 d))" "((a op1 (b op2 c)) op3 d)" "(((a op1 b) op2 c) op3 d)"Putting it all together
We can now generate all combinations of numbers, operators and bracketing by the Cartesian of the three lists:
combos <- cross3( perm, map( operators, unlist), bracketing) %>%
map(setNames, c("numbers", "operators", "bracket"))We can now finally evaluate each of the 1920 combinations. Note:
Because this might take a while it’s a good idea to add a progress
bar for this purrr computation.
##Set up a progress bar for use with the map function
pb <- progress_estimated(length(combos))
##Compute
res <- map(combos, .f=function(l) {
pb$tick()$print()
l[["expr"]] <- l[["bracket"]] %>% replace(l[["numbers"]]) %>% replace(l[["operators"]])
l[["value"]] <- eval(parse(text=l[["expr"]]))
return(l)
})Again, replace(v) is a small helper function to replace
the strings in names(v) with v’s content. The
actual evaluation of each possible solution string is done by parsing
the string with parse and then evaluate the resulting
expression. We extract the relevant results into a
data.frame
df <- map_df(res, ~ data.frame(expr=.x$expr, value=.x$value))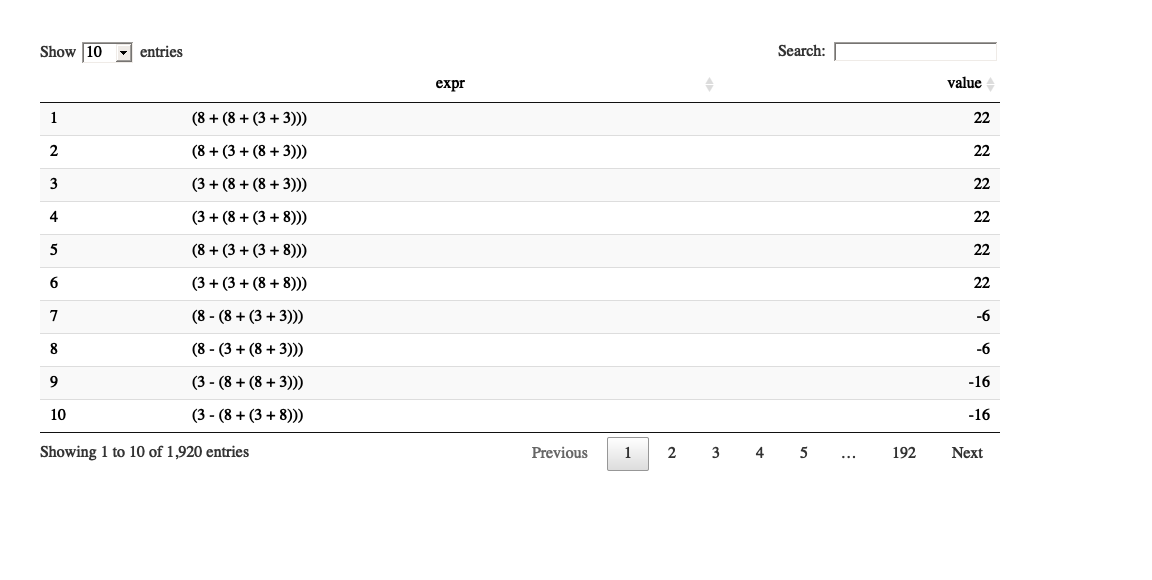
We can now easily extract the solution:
##First element to give the value 24
detect(res, ~ isTRUE(all.equal(.x$value, 24)))## $numbers
## a b c d
## 8 3 8 3
##
## $operators
## op1 op2 op3
## "/" "-" "/"
##
## $bracket
## [1] "(a op1 (b op2 (c op3 d)))"
##
## $expr
## [1] "(8 / (3 - (8 / 3)))"
##
## $value
## [1] 24Voila! QED!
Extended New Years Fun
For user experimentation we wrapped all the above steps into one
function solveMathPuzzle (see github
code for details). To underline the generalizability of the approach
we solve a classical 2019 new-year’s puzzle:
res <- suppressWarnings(solveMathPuzzle( base_numbers=c(7,7,11,11,43,43), expr_result=2019, operatorList=c("+","*")))
res$expr[[1]]## [1] "((7 * 7) + ((11 * 11) + (43 * 43)))"Shiny App
To make the above solution accessible to a wider audience we wrote a small Shiny app to play with the code for \(k=4\):
Here one can alter the input numbers in case variants of the puzzle are in need of a solution or, if you occasionally need to generate math puzzles for your nephew…

Besides possible solutions one can view the result of all possible combinations yielding integer results in the “Details” tab. We invite you to experiment with the app or download the source code of the Shiny app from github for the full math experience. 😃
As always: it’s amazing how easy you can wrap a interactive web based UI around your running R code with Shiny!
Discussion
We used a brute force solution approach by trying out all possible combinations to solve the math puzzle. The code of our solution approach is flexible enough to handle more or less base numbers, however, the number of combinations to try quickly exceeds reasonable memory and timing constraints. We stress that a mathematical purr does not need speed, it lives from the beauty of recursion and mappings! Clever mathematicians might be able to achieve considerable speed gains by exploiting for example commutative properties of the operators whereas skilled computer scientists would parallelise the computations.
Literature
Note: The term \(\frac{1}{k} \binom{2k-2}{k-1}\) is the so called Catalan number, which - among other applications - also denotes the number of ways to parenthesize \(k-1\) binary operations.↩︎
Actually, the package more or less adds a lot of convenience wrapping for functional programming in R, the functional programming approach is rather deeply rooted in R due to the S language being inspired by Scheme.↩︎
A purer functional approach would have been to use the function definition of the operators directly, i.e. to define
operatorListwith elements such as`+`(e1, e2)and then use these functions to build the parse tree as an expression. The disadvantage of such an approach is that the expressions become more cumbersome to write. For example(5 + 3 + 2) * 4as`*`( `+`( `+`(5, 3), 2), 4).↩︎