Retracing Prenatal Testing Algorithms
Abstract
A good understanding of the statistical procedure used to calculate
trisomy 21 (Down syndrome) risk in combined first trimester screening is
a precondition for taking an informed decision on how to proceed with
the screening results. For this purpose we implement the Fetal Medicine
Foundation (FMF) Germany procedure described in Merz et al. (2016). To allow
soon-to-become-parents an insight on what the procedure does and how
sensitive conclusions are to perturbations, we wrote a small Shiny app
as part of the R package trisomy21risk to visualize the
results. We hope the tool can be helpful in the individual decision
making process associated with first trimester screening.

 This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
Introduction
Biostatisticians predominantly analyse samples from populations of dead and diseased in the hope of substantiating answers to question aimed at preventing the adverse event in future individuals. Less common is the personalized \(n=1\) case, where -based on historical data- one has to choose an optimal test sequence or treatment regime for a specific individual. However, when interpreting your own laboratory values that is what you have to do - implicitly or explicitly!
In the case of first trimester prenatal testing for Down syndrome, aka. trisomy 21 (T21), parents are at the end of the screening routine given a piece of paper containing the results of a combined test. This consists of
- the nuchal translucency (NT) measurement (in mm) of the fetus
- concentration of the Pregnancy-associated plasma protein A (PAPP-A) and the human chorionic gonadotropin (β-HCG) hormone in the serum of the mother (measured in miU/ml)
- (optional) results for other markers (e.g. ethnicity, maternal smoking, fetal heart rate, visibility of the nasal bone on the ultrasound)
From the biomarker values NT, PAPPA-A and β-HCG (and possibly additional markers) a risk for T21 is calculated and presented as an odds, say, 1:486. The question for the concerned soon-to-become-parents is now, whether to proceed with further tests - for example a DNA based approach in maternal blood plasma, a so called non-invasive prenatal test (NIPT) or, further down the line, an invasive amniotic fluid test. Recommendations for when to perform which additional screening steps exist and are discussed with the supervising gynecologist, but at the end its your choice as soon-to-become-parents.
The aim of this blog post is to illustrate how we failed to identify and understand the algorithm used to calculate the risk. As a consequence, we attempt a transparent and reproducible risk calculation algorithm based on the procedure described in Merz et al. (2016). To enhance risk communication we wrote an interactive Shiny app to calculate the risk, perform sensitivity analyses and graph distributions. Even though we are not experts on prenatal screening and have no access to any data, we hope such tools can inspire the experts or even be helpful in the individual decision making process associated with first trimester screening.
What is the FMF Algorithm 2012?
The first step in a scientific approach towards the problem is to understand, how the \(y\) in the reported \(1:y\) odds was determined. For this purpose the exemplary result report (in this case from a German prenatal diagnosis facility) contained a cryptic note to a “FMF Algorithm 2012”. Unfortunately, no further reference to any scientific article, no link to a website with additional information nor any separate pamphlet was provided. Nevertheless, the soon-to-be-parents are assured that “The model for calculating the risk is based on intensive research work coordinated by the fetal medicine foundation (registered charity 1037116)”. Cranking the google handle we found that there exists both an UK Fetal Medicine Foundation (FMF), which has the stated registered charity number, as well as a Fetal Medicine Foundation Germany. For reasons unclear to the outsider these two organizations use different risk algorithms: FMF-Germany uses a so called DoE-algorithm (DoE = Degree of extremeness) documented in the Merz et al. (2008), Merz et al. (2011) and Merz et al. (2016) (open-access) sequence of papers. In contrast FMF-UK uses software following “The First Trimester Screening module 2012 algorithm”, which uses so called MoMs (multiples of the median). What this entails we could only find in a rogue access software manual: the document contains a large body of references sketching the different analysis components - in particular Kagan, Wright, Baker, et al. (2008) and Kagan, Wright, Valencia, et al. (2008) seem to cover the essentials components of the algorithm. However, for each component (nuchal translucency, β-HCG, PAPP-A, nasal bone, ductus venosus, heart rate, …) further references are given without it being clear, if or how they enter the algorithm. As an example, the FMF 2012 algorithm seems to analyze the NT measurement by a mixture model approach described in Wright et al. (2008) so the original approach in Kagan, Wright, Baker, et al. (2008) now seems obsolete. This might all be scientifically justified, but for an outsider it is impossible to retrace what is done: Even though we spent quite some time searching the FMF-UK website, which provides access to many of the FMF’s 957 scientific publications and watched videos about the algorithm, we could not find a more coherent document on what the FMF 2012 algorithm exactly is. Even the FMF on-line risk calculator does not contain a specific reference and seems to implement its own a variant of the algorithm (undocumented javascript source code).
At this point it is instrumental to recall paragraph V.3.3 in the Commission on Genetic Testing’s guideline for prenatal screening. It demands that the algorithm for the computation of such risks to be comprehensible, scientifically justified and published in a peer review process. In particular the guideline stresses that scientifically justified means:
With such a strong statement by the guideline about the transparency and reproducibility of the algorithm the above hide-and-seek seems absurd.
Since we at the time of testing (wrongly?) believed that the FMF-Germany algorithm was the one used in the lab report and its papers appeared comprehensible enough for a re-implementation, we decided to scrutinize the FMF-Germany algorithm further in order to understand the computations. Aim was to understand how components influenced the calculation, perform a sensitivity analysis and better understand the uncertainty associated with the reported risk. The FMF Algorithm 2012 was expected to be similar in style.
The FMF-Germany Procedure - PRC 3.0
The procedure described in Merz et al. (2016) entitled Prenatal Risk Calculation (PRC) uses a classic Bayesian diagnostic approach, where one computes a posterior odds for the fetus having T21 as
\[ \text{Posterior odds} = \text{Likelihood ratio} \cdot \text{Prior odds} \]
In the context of T21 first trimester screening, the prior odds is
known to depend on maternal age and gestational age (at the time of
screening) of the fetus. Tables for this can be found in, e.g., Table 4
of Snijders et al.
(1999), which is shown below in the form of odds \(1:x\) for maternal age gaps of 5 years and
selected gestational
ages (measured in weeks). The gestational weeks relevant for the
first trimester screening are the gestational weeks 10-13. Using a
linear interpolation we obtain values for maternal and gestational age
not covered in the table - see the trisomy21risk package
code for details.
| Maternal Age | W10 | W12 | W14 | W16 | W20 | W40 |
|---|---|---|---|---|---|---|
| 20 | 983 | 1068 | 1140 | 1200 | 1295 | 1527 |
| 25 | 870 | 946 | 1009 | 1062 | 1147 | 1352 |
| 30 | 576 | 626 | 668 | 703 | 759 | 895 |
| 35 | 229 | 249 | 266 | 280 | 302 | 356 |
| 40 | 62 | 68 | 72 | 76 | 82 | 97 |
| 45 | 15 | 16 | 17 | 18 | 19 | 23 |
From the table we see that the background risk increases with maternal age and decreases with gestational age. The latter is related to the fact that a T21 fetus has an increased risk of spontaneous abortion. One criticism of using the maternal age as background risk is that age is merely a proxy for processes and complications not well understood. From a certain maternal age, it is thus almost impossible to get a test-negative result, even though most babies born by mothers that age are healthy (Schmidt et al. 2007).
The above formula for the posterior odds means that we can compute the posterior probability for T21 as \[ \text{Posterior probability} = \left( 1 + \frac{1}{\operatorname{LR}_{joint}} \cdot \frac{1-\text{Prior probability}}{\text{Prior probability}} \right)^{-1}. \] The complicated part of the analysis is now to determine the joint likelihood ratio between the aneuploid pregnancies (i.e. T21 pregnancies) vs. euploid pregnancies (i.e. non-T21 pregnancies) as a function of the three biomarkers. In some cases additional continuous or binary markers indicating for example the smoking status, the visibility of the nasal bone on the ultrasound or the ductus venosus blood flow (expressed as pulsatility index) are used to distinguish further. For sake of exposition we use the presence of a nasal bone on the ultrasound as additional marker.
In Merz et al. (2011) and Merz et al. (2016) the likelihood ratio between aneuploid and euploid pregnancies is broken down into individual components by assuming that the random variables describing the observed value for the four risk factors are independent given ploidy (i.e. the T21 status):
\[ \begin{align*} \operatorname{LR}_{joint} &= \frac{f_{\text{aneu}}(y_{\text{NT}}, y_{\beta\text{-HCG}}, y_{\text{PAPP-A}}, y_{\text{nasal bone}})}{f_{\text{eu}}(y_{\text{NT}}, y_{\beta\text{-HCG}}, y_{\text{PAPP-A}}, y_{\text{nasal bone}})} \\ &= \left( \frac{f_{\text{aneu}, \text{NT}}(y_{\text{NT}})}{f_{\text{eu}, \text{NT}}(y_{\text{NT}})} \right) \cdot \left( \frac{f_{\text{aneu}, \beta\text{-HCG}}(y_{\beta\text{-HCG}}}{f_{\text{eu}, \beta\text{-HCG}}(y_{\beta\text{-HCG}})} \right) \cdot \left( \frac{f_{\text{aneu}, \text{PAPP-A}}(y_{\text{PAPP-A}})}{f_{\text{eu}, \text{PAPP-A}}(y_{\text{PAPP-A}})} \right) \cdot \left( \frac{f_{\text{aneu}, \text{nasal bone}}(y_{\text{nasal bone}})}{f_{\text{eu}, \text{nasal bone}}(y_{\text{nasal bone}})} \right)\\ &= \operatorname{LR}_{\text{NT}} \cdot \operatorname{LR}_{\beta\text{-HCG}} \cdot \operatorname{LR}_{\text{PAPP-A}} \cdot \operatorname{LR}_{\text{nasal bone}} \end{align*} \]
In the above, the \(f\)’s denote the respective probability density functions, which may depend on covariates such as gestational age (at the time of measuring) or the weight of the mother. In Appendix 1 we look in detail at how the likelihood ratio is computed for the NT measurement. The procedure is then analogous for the β-HCG and PAPPA-A markers - one difference is, though, that Merz et al. (2016) extends the analysis to allow for these β-HCG and PAPPA serum markers to be collected at a gestational age 2-3 weeks earlier than the NT measurement, because the discrimination is better for these biochemistry markers at this gestational age. Altogether, if the prior odds is given in the form \(1:x\) then \(\operatorname{LR}_{joint}\) is the factor multiplied onto \(x\) to get the posterior odds in the form of \(1:y\). That means that if \(\operatorname{LR}_{joint}>1\) then the marker values are such that the risk for T21 increases.
R Implementation
The trisomy21 function in the trisomy21risk
package performs all the computations to take one from the prior odds,
covariates and biomarker values to the posterior odds.
formalArgs(trisomy21risk::trisomy21)## [1] "age" "weight" "crlbe" "crl" "nt" "pappa"
## [7] "betahCG" "nasalbone" "background"In the above age (in years) and weight (in
kg) refer to the mother, crl is the crown-rump-length
(measured in mm) at the time of the NT measurement and
crlbe is the crown-rump-length at the time of the biomarker
measurement. The pappa and betahCG
concentrations are both measured in miU/ml. Finally,
background is the \(x\) of
the prior odds \(1:x\). The function
outputs a named list of which one element is the posterior odds (in the
form of \(1:y\)).
We can now compare our results to, e.g., the 12 randomly selected patients listed in Tab. 5 of Merz et al. (2016). Note that the first patient has a posterior odds of 1:486, which we used as example patient in the introduction. Results are compared in two ways:
- using the background risk as specified in the
Backgroundcolumn by the paper and comparing our result (Column:our_Post) to the \(y\) of the posterior odds stated in the paper (Column:Post). - Manually calculate the background risk using maternal age and
gestational age by interpolation of the Snijders table (Column:
our_Background) and compare our result (Column:our_Post_Back) with the result of the paper (Column:Post).
##Load numbers from Tab. 5 of the paper (contains 12 patients)
tab5 <- read.csv2(file.path(filePath,"merzetal2015-tab5.csv"))
##Compute our own results for each patient
tab5 %<>% rowwise %>% do({
##Arguments for the call to the trisomy21 function
args <- list(age=.$Age, weight=.$Weight, crlbe=gestage2crl(.$CRLBE), crl=gestage2crl(.$CRL), nt=.$NT, pappa=.$PAPP_A, betahCG=.$beta_hCG, nasalbone="Unknown", background=.$Background)
##Manually compute the prior odds
our_Background <- background_risk(age_mother=.$Age, gestage=.$CRL/7)
##Call the trisomy function with the two type of background odds
post <- do.call("trisomy21",args=args)
post_back <- do.call("trisomy21",args=modifyList(args, list(background=our_Background)))
##Return result
data.frame(., our_Post = post$onetox, our_Background=round(our_Background,digits=0), our_Post_Back=post_back$onetox)
})| Age | Weight | CRLBE | CRL | NT | PAPP_A | beta_hCG | Background | Post | our_Post | our_Background | our_Post_Back |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 74.5 | 58 | 86 | 2.3 | 0.330 | 52.5 | 145 | 486 | 494 | 140 | 477 |
| 33 | 65.1 | 58 | 86 | 2.0 | 0.526 | 124.7 | 349 | 1022 | 1043 | 352 | 1052 |
| 27 | 48.6 | 59 | 88 | 1.2 | 0.210 | 71.6 | 876 | 2901 | 3412 | 752 | 2931 |
| 23 | 65.4 | 58 | 88 | 1.9 | 0.725 | 96.0 | 1021 | 13238 | 13583 | 915 | 12175 |
| 42 | 72.8 | 59 | 89 | 2.0 | 0.359 | 77.0 | 45 | 176 | 208 | 35 | 162 |
| 37 | 69.0 | 58 | 89 | 1.8 | 0.241 | 47.2 | 147 | 1355 | 1526 | 140 | 1453 |
| 36 | 84.4 | 58 | 90 | 2.0 | 0.290 | 51.9 | 225 | 2198 | 2332 | 180 | 1865 |
| 41 | 61.6 | 55 | 90 | 1.7 | 0.219 | 84.6 | 55 | 264 | 285 | 47 | 243 |
| 30 | 57.6 | 59 | 91 | 1.6 | 0.349 | 75.3 | 677 | 6329 | 6990 | 576 | 5947 |
| 26 | 64.7 | 59 | 92 | 1.6 | 0.230 | 73.9 | 945 | 3983 | 4506 | 811 | 3868 |
| 35 | 74.3 | 59 | 92 | 1.5 | 0.399 | 69.6 | 233 | 5072 | 5691 | 229 | 5593 |
| 34 | 51.6 | 58 | 93 | 2.1 | 0.563 | 142.4 | 338 | 902 | 966 | 287 | 821 |
Altogether, we observe that the results do not fully agree, but are
in most cases of the same magnitude. Even when using the same prior odds
there are still differences, which can be explained by the use of
different polynomial \(\hat{y}(x)\)
forms for NT, PAPP-A and β-HCG, because of problems reproducing the
results with the polynomials stated in Merz et al. (2016) - see Appendix
2. Furthermore, the interpolation of the background risks from the
Snijders table (Column: our_Background) deviates:
Apparently, a different interpolation procedure is used by Merz et al. (2016) -
we could not find an explicit mentioning of how this part is done.
Shiny App
For better illustration we have written a small Shiny app in order to get a better feeling of what the algorithm does, for example, by performing a sensitivity analysis where one changes one measurement value slightly. The App is available from:
and can also be ran locally, by installing the trisomy21risk
package from github:
devtools::install_github("hoehleatsu/trisomy21risk")
trisomy21risk::runExample()Screenshots
Computing the T21 risk: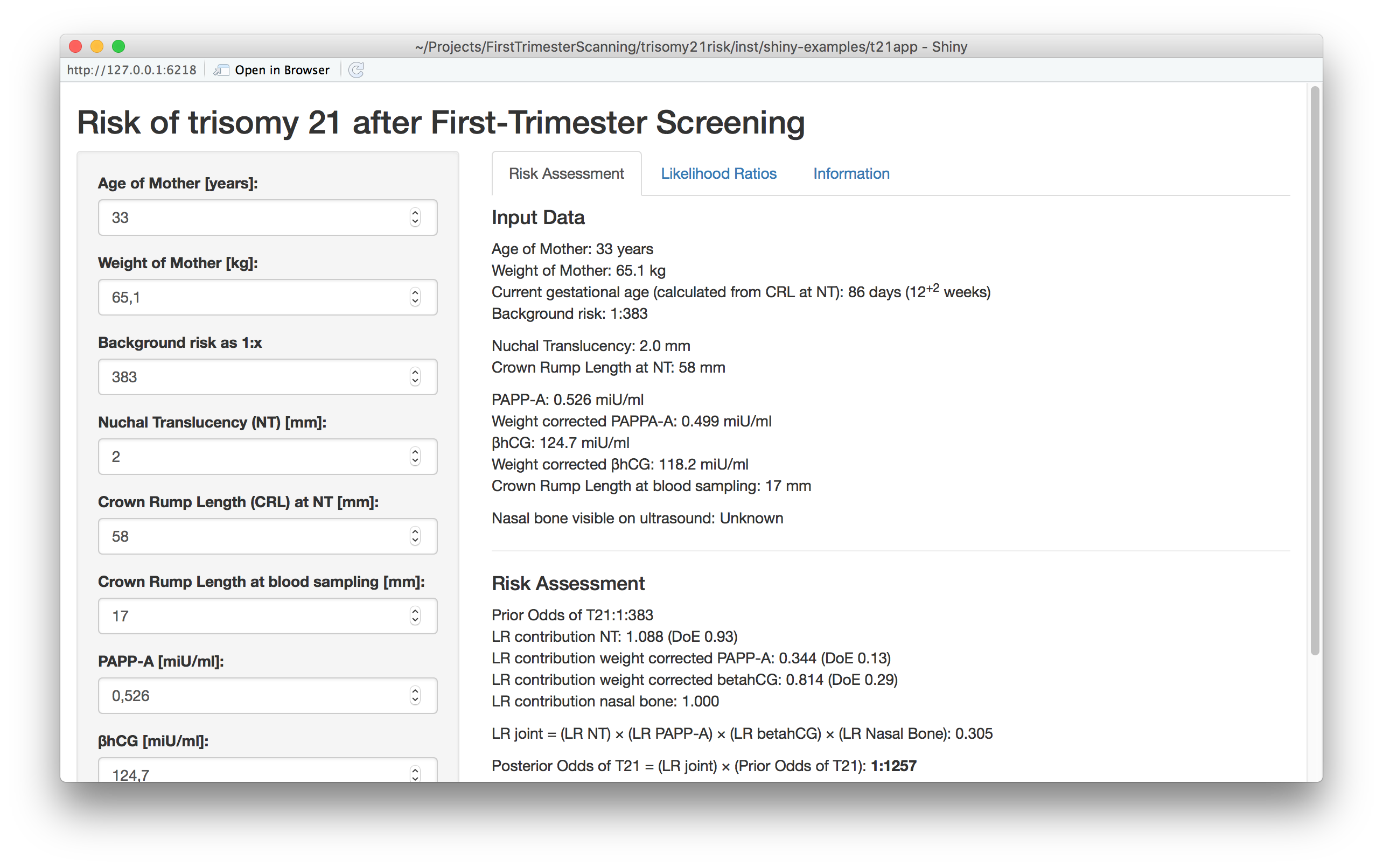
As example: the NT measurement in the ultrasound image is subject to some measurement error - even the most skilled operator has difficulties obtaining errors smaller than 0.2 - 0.3 mm. With the app we can easily investigate how such measurement error influences the calculated risk. Another aspect to investigate is the influence of the background risk from maternal age.
Visualizing the likelihood ratios: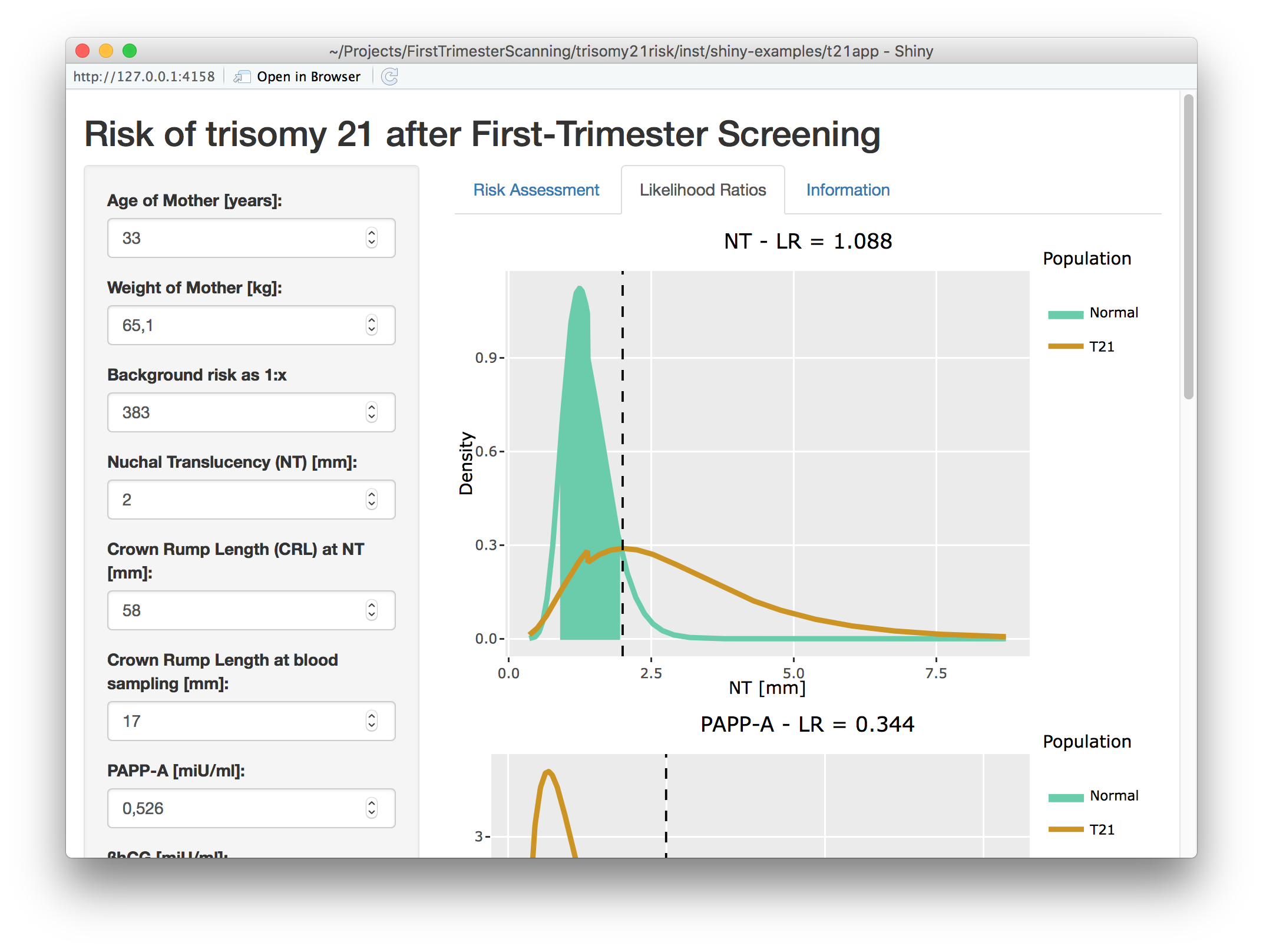
Discussion
With a cut-off of value of 1:150 for the posterior odds, Merz et al. (2016) report a detection rate for T21 of 86.8% and a false positive rate of 3.42%. The 1:150 is also the threshold they suggest for further invasive action. For posterior odds up to 1:500 the suggestion in Merz et al. (2011) is to perform additional sonographic investigations in the second trimester. Nowadays, one would typically perform a NIPT.
Was the algorithm for the computation of the risk detailed and comprehensive as demanded by the Commission on Genetic Testing? Well, since we -despite quite some effort- were not able to find a full description of the FMF 2012 algorithm and, as described in Appendix 2, were not able to reproduce the numbers in Merz et al. (2016), we say: no. As algorithms become more complex and -as for the FMF 2012 algorithm- contain the combined insights of 10+ scientific papers, transparency starts with a single easy-to-find accessible document coarsely describing the overall algorithm. The FMF software manual, which apparently is not accessible to the public, would have been a start. Even better would be an open-source reference implementation! To this date it remained unclear how the standard NT, PAPP-A and β-HCG measurements entered the analysis and if additional components (ethnicity? smoking status? nasal bone? heart rate? ductus flow?) entered the risk calculation. Similarly, publishing a statistical description of the FMF-Germany algorithm in open-access articles, e.g. such as Merz et al. (2016), is a step in the right direction, however, some of the equations in the paper were either erroneous or intentionally kept so vague, the algorithm became impossible to reconstruct. Altogether, transparency and risk communication for this sensitive diagnostic procedure should be improved to meet guideline standards.
What do you do with the obtained posterior risk once you have it? This is indeed a very personal decision, which make the shortcomings of statistics clear: Statisticians can annotate even the most unlikely event with a probability of happening, but the probability is rarely zero, so it’s your personal threshold for likely enough balanced against the ethics and personal beliefs of what to do if, which determines your actions… In this \(n=1\) context the reported risk might merely be a hypothetical number - at most its rough magnitude is of interest. However, from a system perspective \(n\) is much larger, so everything possible should be done such that the probabilistic forecast is both calibrated and sharp and that the recipient(s) knows what this number entails.
Postscript
Further information about first trimester screening can be obtained from the Fetal Medicine Foundation. In particular their book about the 11-13 weeks scan (available in several languages) is very helpful (Nicolaides 2004). As mentioned the FMF-UK offers a web-based trisomies risk assessment calculator. Similarly, the FMF-Germany has their own website with information - apparently it is now also possible to obtain a demo version of their risk calculation software PRC 3.0.
Update 2018-07-24
Directly after publishing the post I contacted the German Commission on Genetic Testing (GEKO) to make them aware of the post and my troubles to determine what the algorithm actually does, what information enters and the lack of will of the FMF-Germany authors to communicate certain details of the algorithm. As a consequence, I asked which steps the commission performs to ensure and track the realisation of the guideline’s demands for “publication of the entire algorithm with detailed software specification”. In their email reply from 2018-07-16 they answer1: “… The area of responsibility of the GEKO is clearly regulated by legal requirements. The implementation of the Gene Diagnostic Act (GenDG) or the examination of the guideline’s requirements are not tasks of the GEKO. The interpretation of the regulatory content of the Gene Diagnostic Act as well as the enforcement of the requirements of the GEKO guidelines are dealt with by the appropriate authorities of the Länder.” As a consequence of this, their recommendation was to address my question to the equivalent of the Ministry of Health in my federal state (Berlin). I did this on 2018-07-16 (awaiting reply), but would be surprised, if the Federal State of Berlin has the resources and expertise to look into software transparency of national and internationally operating software vendors in this field. I doubt this is different for any of the 15 other federal states in Germany. I might be wrong and in for a surprise, but as a citizen and scientist it seems like the guideline’s demand for a detailed software specification in order to make it transparent and reproducible how the 1:x is calculated is nothing else than wishful thinking…
Update 2019-03-29
After several inquiries about what is done to ensure the algorithmic transparency of the prenatal diagnostic procedures remained unanswered by Berlin’s Senatsverwaltung für Gesundheit, Pflege und Gleichstellung, I decided to formulate a freedom of information act request, which ensures that the public authority has to answer, typically within ~4 weeks. A very good interface to formulate such requests in Germany is fragdenstaat.de. The subsequent answer (in German) shows that no measures are performed in Berlin to ensure the requested algorithmic transparency. My conclusion: The current setup of a) recommendations being in the hand of the GEKO while b) compliance assurance being in the hand of 16 federal states results in the software providers not being under any pressure to provide algorithmic transparency. This is rather frustrating for an ethical sensitive issue such as prenatal screening.
Appendix
The mathematical details of the post and our troubles reproducing the results of Merz et al. (2016) are described in two separate Appendixes,
Literature
My email and their answer was in German - the quoted part of the answer is translated to English by me.↩︎