When Should One Stop Testing Software?
Abstract
This is a small note rediscovering a gem published by S. R. Dalal and C. L. Mallows on treating the test of software in a statistical context (Dalal and Mallows, 1988). In their paper they answer the question on how long to continue testing your software before shipping. The problem is translated into a sequential decision problem, where an optimal stopping rule has to be found minimizing expected loss. We sketch the main result of their paper and apply their stopping rule to an example using R code.
 This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
Introduction
Imagine that a team of developers of a new R package needs to structure a test plan before the release of the package to CRAN. Let \(N\) be the (unknown) number of bugs in the package. The team starts their testing at time zero and subsequently find an increasing number of bugs as the test period passes by. The figure below shows such a testing process mimicking the example of Dalal and Mallows (1988) from the testing of a large software system at a telecommunications research company.

We see that the number of bugs appears to level off. The question is now how long should we continue testing before releasing? Dalal and Mallows (1988) give an intriguing statistical answer to this problem.
Methodology
In order to answer the above question the following notation and assumptions are introduced:
The total number of bugs is assumed to be Poisson distributed \[N \sim \text{Po}(\lambda).\] However, practice shows that the number of bugs in different modules has more variation that given by the Poisson distribution. Hence, let \(\lambda \sim \text{Ga}(\alpha,\beta)\) and thus the marginal distribution of \(N\) is negative binomial.
The amount of time until discovery of each bug during the testing period is distributed according to the known distribution \(G\) with density \(g\). Furthermore, it can be assumed that the discoveries times are independent of each other. Example : The simplest example is to assume that the discovery distribution is exponential, i.e. \(g(t)=\mu\exp(-\mu t)\), where we measure time in number of person-days spent on the testing. Thus, \(1/\mu\) is the expected time until discovery of a bug.
Let \(K(t)\) be the total number of bugs found up to time \(t\). In other words, if \(t_1,\ldots,t_N\) denote the discovery times of the \(N\) bugs then
\[K(t)=\sum_{i=1}^N I(t_i \leq t),\]
where \(I(\cdot)\) is the indicator function. However, note that at time point \(t\), only bugs with a discovery time smaller or equal to \(t\) would already have been observed and, hence, would be known to exist (right-truncation). Thus, even though \(K(t)\) is proportional to the empirical cumulative distribution function of the discovery distribution \(\hat{G}(t)\), the factor of proportionality is \(N\), which is unknown at the time \(t\).
Note: The paper actually showns that the Poisson-Gamma distribution assumption for \(N\) is not crucial. An asymptotic argument is given that as long as the process does not terminate quickly (i.e. the number of bugs is relatively large) the results hold for more general distributions of \(N\). Hence, in the analysis that follows, the parameter \(\lambda\) is not needed as we only proceed with the asymptotic approach of the paper.
Loss function
In order to make a decision about when to stop testing based on expected loss/gain we need two further assumptions:
Let \(c\) be the net cost of fixing a bug after release of the software instead of before the release. Hence, \(c\) is the price of fixing a bug after release minus the price of fixing a bug before release. The practice of software development tells us that \(c>0\).
Let \(f(t)\) be a known non-negative and monotone increasing function reflecting the cost of testing plus the opportunity cost of not releasing the software up to time \(t\). Note that the cost of testing does not contain the costs of fixing bugs, once they are found. A simple example for \(f\) is the linear loss function, i.e. \(f(t) = f \cdot t\), where \(f>0\) is a known constant.
The above assumptions in summary imply the analysis of the following loss function:
\[L(t,K(t),N) = f(t) - c K(t) + b\cdot N.\]
As time passes, one obtains information about the number of bugs found through \(K(t)\). At each time point the following decision has to be made: stop testing & ship the package or continue to test. Seen in a statistical context this can be rephrased into formulating a stopping rule such that the above loss function is minimized.
Optimal Stopping Time
In the simple model with exponential discovery times having rate \(\mu\), the stopping rule stated as equation (4.6) of Dalal and Mallows (1988) is to stop as soon as the number, \(k\), of bugs found at time \(t\), i.e. \(K(t)=k\), is such that:
\[ \frac{f}{c}\cdot \frac{\exp(\mu t) -1}{\mu} \geq k. \]
At this time point, the estimated number of bugs left is Poisson with mean \(f/(c\mu)\).
##########################################################################
# Function describing the LHS of (4.6) in the Delal and Mallows article
#
# Parameters:
# fdivc - the quotient f/c
# mu - the value of mu, this typically needs to be estimated from data
# testProcess - a data_frame containing the decision time points and the
# observed number of events
##########################################################################
lhs <- function(fdivc,mu,testProcess) {
fdivc*(exp(mu*testProcess$t)-1)/mu
}In the above, the quantity \(c/f\) measures the amount saved by finding a bug (and hence fixing it before release) measured in units of testing days. As an example: if \(c/f=0.2 \Leftrightarrow f/c=5\) then the gain in detecting a bug before release corresponds to 0.2 testing days. Throughout the subsequent example we shall work with both \(c/f=0.2\) (ship early and fix later is acceptable) and \(c/f=1\) (high costs of fixing bugs afte r the release).
Example
Taking the testing data from the above figure, the first step consists of estimating \(\mu\) from the available data. It is important to realize that the available data are a right-truncated sample, because only errors with a discovery time smaller than the current observation time are observed. Furthermore, if only data on the daily number of bug discoveries are available, then the data are also interval censored. We set up the loglikelihood function accordingly.
#######################################################
#Log-likelihood function to maximize, which handles the
#right truncation and interval censoring.
# Paramers:
# theta - \log(\mu).
# testProcess - data_frame containing the observed data
# tC - the right-censoring time.
########################################################
ll <- function(theta, testProcess, tC=max(testProcess$t)) {
mu <- exp(theta)
#Daily number of *new* bug discoveries. .
DeltaK <- c(0,diff(testProcess$K))
#CDF function taking the right-truncation into account
CDF <- function(x) pexp(x,rate=mu)/pexp(tC,rate=mu)
#Log-likelihood is equivalent to multinomial sampling with p being a func of mu.
p <- CDF(1:(max(testProcess$t)+1)) - CDF(testProcess$t)
return(sum(DeltaK * log(p)))
}
#Find MLE
mle <- optim(log(0.01),ll, testProcess=testProcess, control=list(fnscale=-1),method="BFGS")
mu.hat <- exp(mle$par)
c(mu=mu, mu.hat=mu.hat)## mu mu.hat
## 0.02000000 0.01916257Note that we in the above used all data obtained over the entire testing period. In practice, one would instead sequentially update the \(\mu\) estimate each day as the information arrives – see the animated sequential procedure in the next section.

## Source: local data frame [1 x 5]
##
## t K K_estimate sol5 sol1
## (int) (dbl) (dbl) (dbl) (dbl)
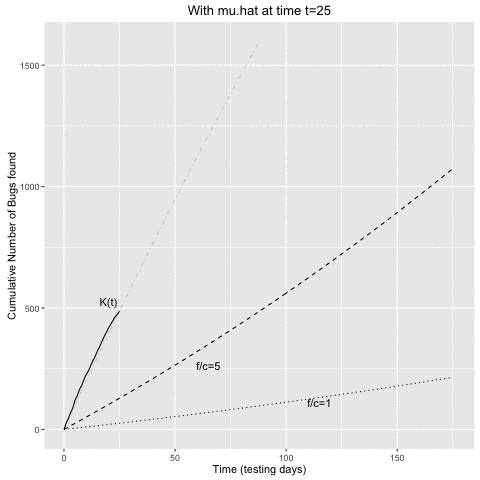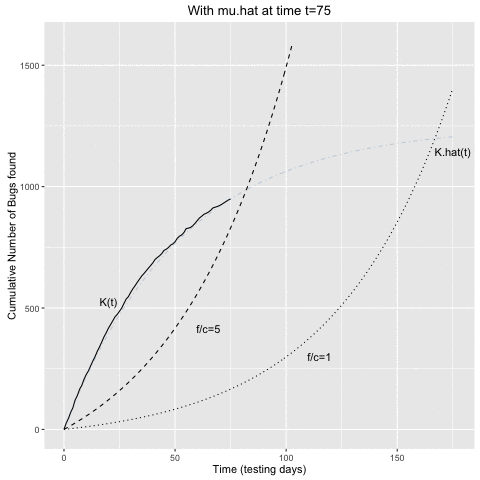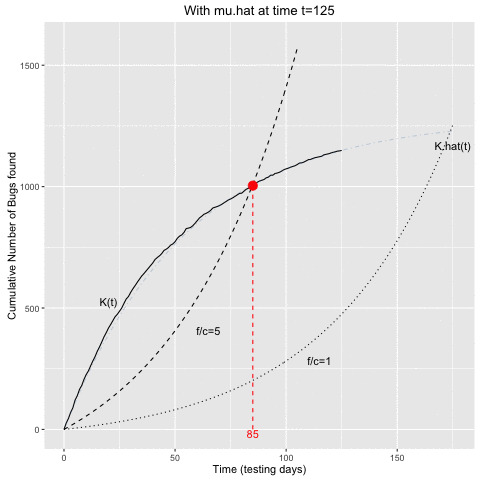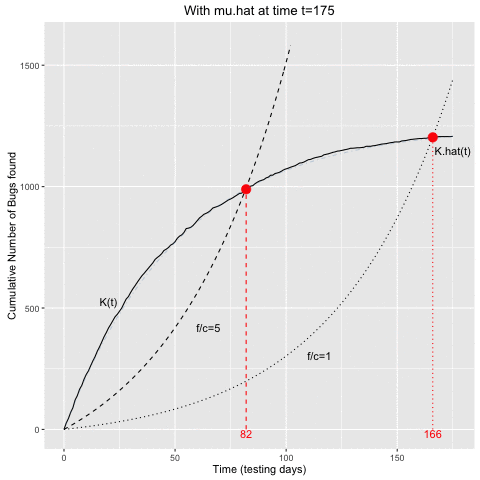
## 1 82 989 990.8676 994.9211 198.9842The optimal stopping time in the example, in the case of \(f/c=5\), is to stop the testing after 82 testing days. An estimate of the expected number of remaining bugs at this stopping time would be 260.9, which appears to agree quite well with the empirical data – actually, they were simulated with \(N=1250\).
Animation
The animation belows shows the above computations in sequential fashion:
- At a given time \(t\) of the testing process, \(\hat{\mu}\) is determined from the curve of cumulative bugs found up to time \(t\).
- This \(\hat{\mu}\) estimate is then use to determine the intersecting curves as described above.
- Once the \(K(t)\) curve and the curve for a given \(f/c\) ratio intersect, we would stop the testing.
Discussion
Assuming that the time periods until discovery of the bugs are independently distributed appears convenient, butnot so realistic. The paper has a section about analysing the situation in case of different classes of bugs. However, fixing a bug often spawns new bugs. Hence, the bug-process could instead be more realistically modelled by a self-exiciting process such as the Hawkes’ process (Hawkes, 1971).
For Open Source Software and in particular R packages, which nobody might ever use, is \(c\) really bigger than zero? Ship and fix might be a good way to test, if a package actually addresses any kind of need?
How to extract the daily number of bugs found from your bug tracking ticket system?
Literature
Dalal, S. R. and C. L. Mallows. “When Should One Stop Testing Software?”. Journal of the American Statistical Association (1988), 83(403):872–879.
Hawkes, A. G. “Spectra of some self-exciting and mutually exciting point processes”. Biometrika (1971), 58(1):83-90.